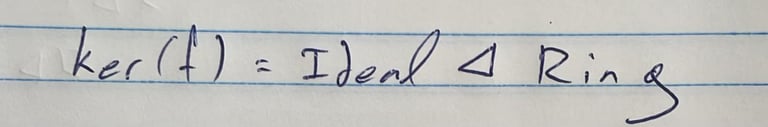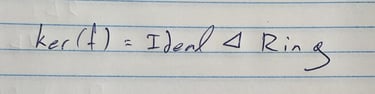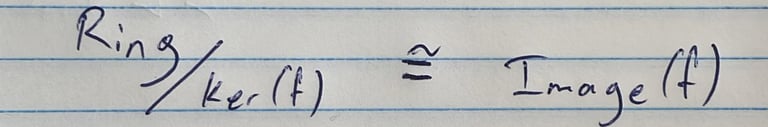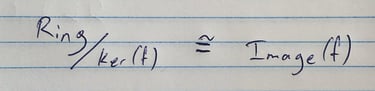אבל את כל זה יש גם בחוגים אחרים. החלק החשוב בחוג הזה הוא שלא כולם אפסים ולא כולם אדישים ושהם עובדים יחד ומתעסקים במתמטיקה מעשייתית, שנמצאת ממש בחיתוך שבין כמה מתמטיקות חשובות: הטהורה, השימושית והניסיונית.

תשתית אידאולוגית

לב העניין הוא בניסיון לקשר את החוג לעולם באופן משמעותי. ועדיף באופן שמשמר מבנה באיזושהי צורה.

אם מצליחים לשמור גם על גרעין של אמת, אז אפשר להתחיל לזהות כמה אידאלים שיכולים לכוון אותנו באפלה.

ואז, לפי התורה, נוצרים כבר מבנים שאיכשהו מצליחים לתאר את תמונת העולם שלנו, או לפחות איזושהי תמונה.

ומפה מתקדמים בצורה רקורסיבית.

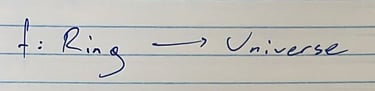
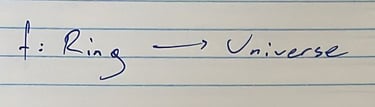
שלד מודולרי

הצעד הראשון הוא להרים את הראש, וזה לא כל כך פשוט בזמן האחרון. אבל ברגע שמצליחים לעשות זאת אפשר לראות שמעל החוג יש מודול עצום ורב מימדי ובו אטומים ומולקולות ותאים ויצורים ואנשים ומחשבים ועוד המון דברים.

ובין כל אותם דברים יש יחסים, והם יוצרים קבוצות וגם עושים יחד פעולות, וככה נוצרות חבורות.

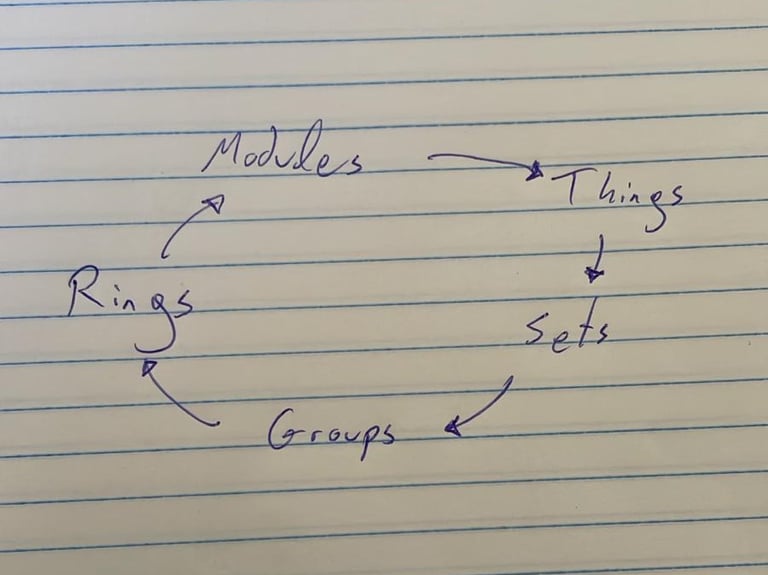
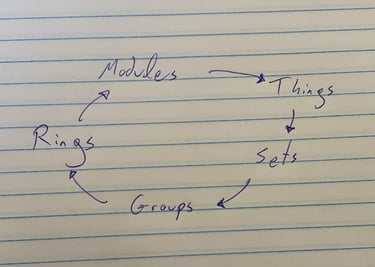
ולפעמים, בעיקר כשהם נפגשים באופן תדיר ומצליחים לממש פעולה משותפת נוספת, נוצרים גם חוגים ומעליהם מודולים ובהם עוד דברים וככה זה ממשיך עוד ועוד.

החלק המעניין הוא שכל המבנים המופשטים האלו פועלים אלו על אלו, ויחד הם יוצרים, לפי התורה, מין הצגה משונה של המציאות שמאפשרת להבין אותה באיזשהו אופן, וזה נחמד כי אז אפשר להרים את הראש אפילו עוד קצת, וממבט הציפור אפשר כבר להתחיל לזהות את הבעיה.

הגדרת הבעיה

הבעיות מתחילות כשהמבנים מתחילים לפתח מודעות משל עצמם ולשים לב שחלק מהמבנים האחרים פועלים בצורה שאינה מכבדת את המבנה הפנימי שלהם. ואם להיות ספציפיים - הבעיה שלנו מתחילה כשפעולות של מבנים אחרים לא מכבדות את האידאלים של החוג.

אז הנה אידאל:

(I) לבנות מערכות חברתיות טובות יותר

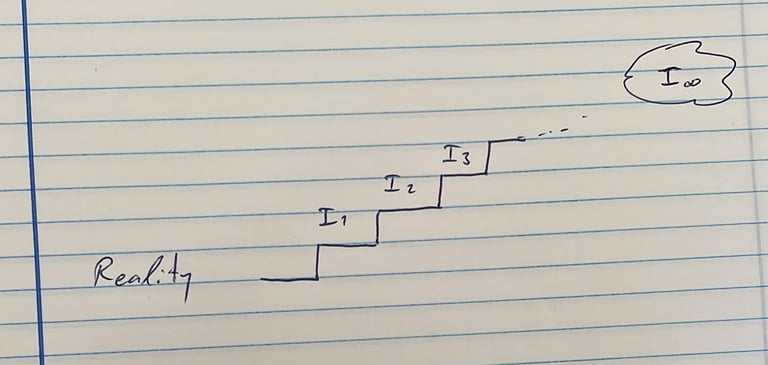
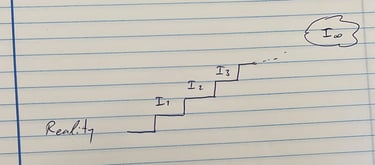
וזה באמת אידאל יפה, אבל הוא עדיין קצת באוויר, וגם קצת חורג מתחומי המחקר של החוג שלנו, אז כדאי אולי להתחיל בזה:

(I1) לזהות מבנים מתמטיים שתומכים במערכות חברתיות אלטרנטיביות

כי אחרי שעושים את זה אז הדברים קצת יותר יציבים ואפשר להתקדם לאידאלים נוספים כמו:

(I2) לתכנן מודלים חישוביים שתומכים במערכות אלטרנטיביות

או:

(I3) לעצב מודלים כלכליים שתומכים במערכות אלטרנטיביות

וככה להתקדם בהדרגה ולקרב את הגאולה.

אבל צעד צעד. נתחיל ביסודות.

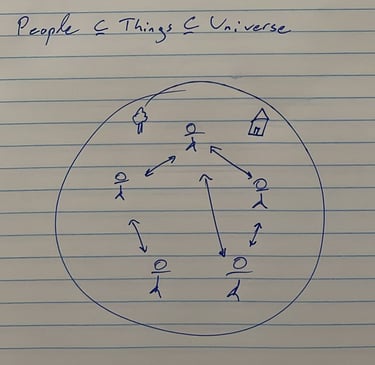
קבוצות ויחסים

אז יש עולם, ויש בו כלמיני דברים וגם אנשים, ועכשיו ניזהר מאוד שלא לחלק אותם לקבוצות של יהודים וערבים ודתיים וחילונים וימנים ושמאלנים ודרוזים ובמקום זה נתמקד ביחסים בינהם, כי היחסים האלו יהיו אבני הבניין הבסיסיות שלנו.

ונתחיל באקסיומה פשוטה אבל עמוקה:

(A1) אין אנשים טובים ואנשים רעים, אבל יש בינהם יחסים מכלמיני סוגים

וכדי לפשט נתחיל עם חלוקה בינארית ליחסי משיכה ויחסי דחייה.

מתישהו כבר נסבך את זה יותר.

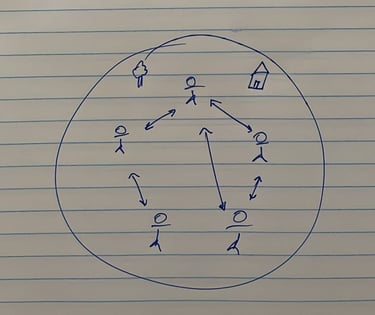
גרפים מסומנים

את האנשים נתאר כנקודות (או - "קודקודים") ואת היחסים נתאר בעזרת קווים שמחברים בינהם ("צלעות") ומכל שאר הדברים נתעלם כרגע ומה שנקבל זה גרף לא מכוון שמתאר את המבנה הבסיסי שאנחנו מתחילים ממנו עם צלעות מסומנות לפי טיב היחסים (+\-).

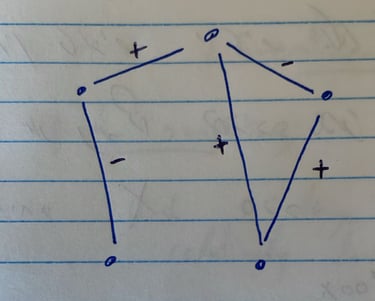
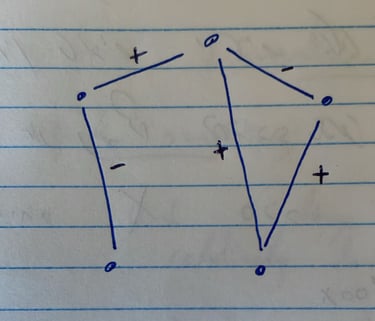
מרחבים ושיכונים

עכשיו נחפש איזה מרחב נעים שמאפשר חופש פעולה, ואולי גם עוד כמה פעולות חדשות שאפשר לעשות. ועדיף גם כזה שמגיע עם נורמות שאפשר לחיות איתן (להבדיל למשל מהנורמה של לדרוך על מישהו אחר כדי לטפס במעלה הפירמידה).

אז ניקח את הגרף שלנו, נוודא שהוא עומד בתנאים מסוימים (ואם לא, נשנה אותו קצת...), ואז נשכן אותו במרחב אוקלידי רב מימדי כך שצלעות [+] יתפקדו כאלמנטי דחיסה (מוטות), צלעות [-] יתפקדו כאלמנטי מתיחה (כבלים), ושהמערכת כולה תהיה בשיווי משקל.

המבנה שנקבל נקרא מבנה עוצמתיחות, כי יש לו גם עוצמה וגם מתיחות (באנגלית, tensegrity = tension + integrity). והנה - יש לנו מבנה מתמטי יציב שמכבד את היחסים הפנימיים בין הרכיבים שלו, כי צלעות מסוג מסוים מושכות את הקודקודים שלהן זה אל זה וצלעות אחרות שומרים על מרחק ומעניקות נפח למבנה.

ויש גם דרך חישובית לא מאוד מסובכת לבצע את השיכון הזה.

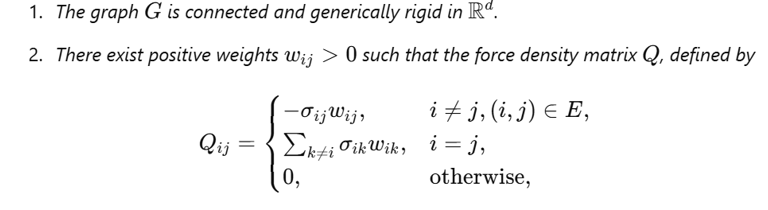
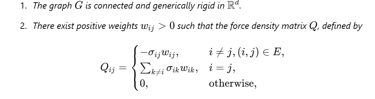
מערכות חברתיות אלטרנטיביות

אז בעצם רק נשאר להראות שאפשר לבנות מערכות חברתיות על בסיס המבנים האלו. אבל את זה אנחנו בעצם כבר יודעים, כי בסופו של דבר, כל מערכת חברתית היא בסה"כ מכונת טיורינג,

ולפי

Church-Turing thesis: Anything computable by a centralized Turing machine can also be computed by a distributed system of Turing machines, given enough time and coordination.

- This assumes unbounded time, perfect reliability, and complete communication.

❌ Practically: Not Always

1. Communication limits:

- Distributed nodes must coordinate, which takes time and bandwidth.

- Latency and network partitions can cause inconsistency.

אנחנו בעצם מחפשים מבנים חזקים וגמישים שיחליפו את הפירמידות העתיקות האלו,

מרחבים ונורמות

ורק עכשיו, כשיש כבר מבנה שמגיע משוכן בתוך מרחב , עם נורמות קצת יותר מכובדות מהנורמות המקובלות במחוזותנו, וכמה פעולות חדשות שאפשר לעשות, עכשיו אפשר לחלק לקבוצות. או יותר נכון - קהילות, כי כבר יש בהן מבנה ויחסים.

הפעולה הקהילתית הראשונה שאפשר לעשות היא להגדיר את מרכז המסה של הקהילה - נגיד בתור הממוצע של שיכוני הקדקודים של החברים בקהילה (אבל יש עוד אפשרויות).

בעצם רק

אנחנו בעצם מחפשים מבנים חזקים וגמישים שיחליפו את הפירמידות העתיקות האלו,